Key Takeaways:
- The paraxial approximation simplifies optical calculations by assuming small angular deviations, useful for systems like lasers and optical fibers. It’s accurate for angles under 10 degrees, where errors are less than 0.5%, but fails at larger angles, requiring more precise methods.
- For waveguides with small effective mode areas or strong focusing systems, the approximation becomes unreliable.
- In such cases, more advanced techniques are necessary, including distinguishing between meridional and sagittal rays or using beam propagation methods for precise results.
Understanding the Paraxial Approximation
The paraxial approximation (approximation at small angles) is a useful mathematical trick for doing ray tracing and simplifying optical calculations. It assumes that angular deviations in propagation from a beam axis are minimal, and is a key part of the optical designer’s toolbox, especially when it comes to laser physics and fiber optics.
But it’s important to check and double-check to be sure that this approximation is valid for your optical system. While this approximation works well for many small angles, it becomes more and more problematic as paraxial ray angles increase. If you utilize the paraxial approximation where it doesn’t apply you may end up with a system that performs very differently in practice than it did on paper.
This article is the sixth part of a multi-part series on common mistakes in the paraxial optics industry. Each article will look at a topic that is often confused, and provide a brief, easy-to-understand explanation of the key foundational concepts involved.
What is the Paraxial Approximation?
In geometrical paraxial optics we consider that light is propagated in the form of geometric paraxial rays. When we do this, the paraxial approximation allows us to assume that this propagation doesn’t deviate much from the propagation axis. More specifically, we can assume that the tangent and sine of all angles are the same as the actual angles, in radians. We could write this:
tan(u) = u and sin(u) =U
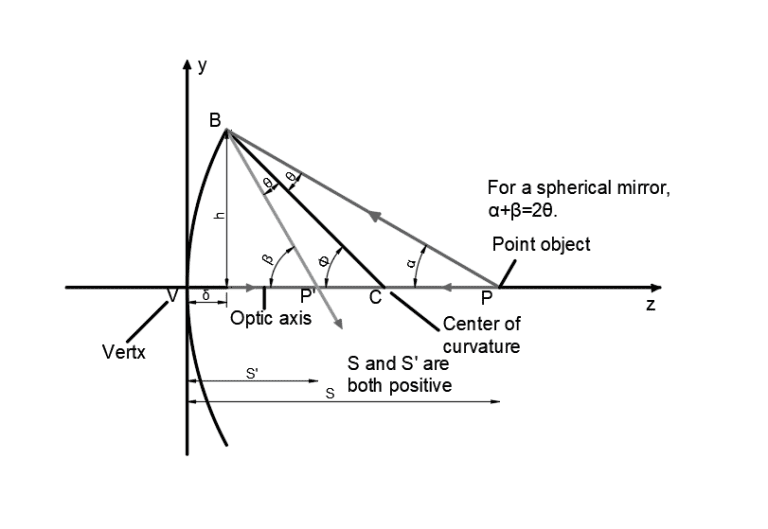
This is illustrated below for an optical system in which the index of refraction goes from n to n’ at the y-axis. In the system below the paraxial approximation allows us to assume that sin(i) = I, sin(I’)=i, sin(u)= u, and sin (u’) = u’.
When Does the Paraxial Approximation Not Apply?
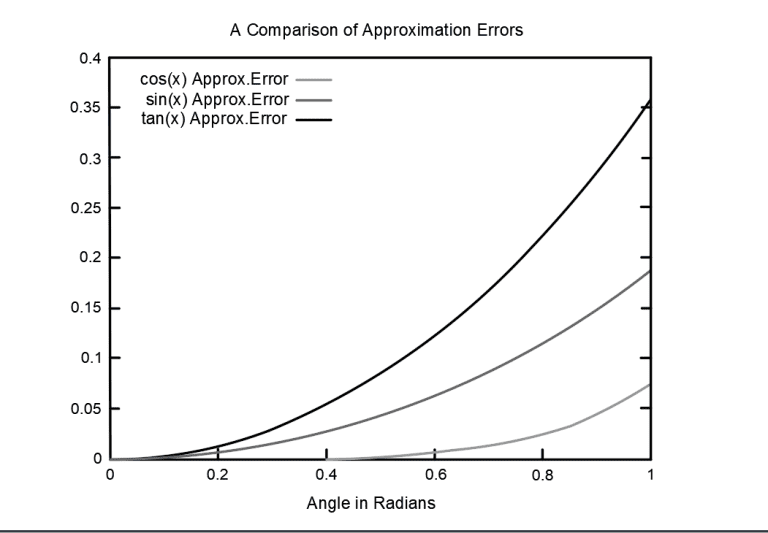
The paraxial approximation is a suitable choice in many situations in which one might be working with small angles; with light rays close to the optical axis. In general, it can be considered a good approximation (deviating by no more than 0.5%) if the angle is under 10 degrees.
But what happens when the angle gets larger? Then the paraxial approximation is no longer valid, and you’ll need to do more explicit calculations. When you’re working with large angles you may need to distinguish between those angles that lie on a plane with the optical axis—- we call these meridional rays— and those that are on another plane, sagittal rays.
One situation in which the paraxial approximation is often used is in the analysis of propagation modes of waveguides for optical fibers. When divergence in the beams exiting a given wavelength is small and the effective mode area is large, this approximation leads to simple, straightforward calculations and an accurate estimate of how the light will propagate. The paraxial approximation shouldn’t be used with large beam divergence or with a small effective mode area.
Another area in which you can’t use the paraxial approximation is when working with extra strong focusing. In this situation it isn’t only the large angle that complicates the issue; polarity also cannot be ignored. For optical systems with very strong focusing, you will want to use beam proportions methods that involve a two-dimensional array of complex field amplitudes rather than the paraxial approximation.
![Paraxial approximation is key to ray tracing in many fields, but it’s important to be aware of when it works— and when it doesn’t]](https://avantierinc.com/wp-content/uploads/2024/10/Understanding-the-Paraxial-Approximation-3-768x269.png)
Ray Tracing and Optical Design at Avantier
When you work with optical designers and engineers at Avantier, you know you’re working with world-class experts. Our optical engineers can walk you through important design considerations for your application, and help you determine whether or not the paraxial approximation applies in your case. More than fifty years working on optical systems like yours have given our teams the know-how to avoid optical pitfalls and design effective, high-quality optical systems that provide you with the ultimate performance you need. Contact us today to set up your first consultation or place a custom order.
GREAT ARTICLE!
Share this article to gain insights from your connections!





