Key Takeaways:
- The guide details the mirror equation, distinguishing between concave and convex spherical mirrors based on their curvatures and radius of curvature.
- It explains how concave mirrors converge light rays to form real, inverted images, contrasting with convex mirrors that diverge rays to create virtual, upright images.
- Sign conventions are essential for understanding spherical mirrors, defining positive and negative distances and heights relative to the principal axis, crucial for accurate optical calculations.
Introduction to Spherical Mirrors: Concave and Convex Mirror Characteristics
In “Understanding Concave and Convex Mirrors”, concave mirrors are defined as curved reflective surfaces that converge parallel rays of light, with characteristics varying based on the object’s position relative to the mirror. Five cases are outlined, detailing the formation, orientation, and size of images. Convex mirrors, on the other hand, possess outward-curving reflective surfaces, causing parallel rays to diverge. The description emphasizes that images formed by convex mirrors are always virtual, upright, and reduced in size, with no real focal point. The guide provides essential terms like pole, center of curvature, and principal focus, offering a foundational understanding of concave and convex mirrors.
We begin by inviting readers to envision a glass sphere with a reflective inner surface, introducing the concept of spherical mirrors. The text categorizes these mirrors into concave and convex types, providing a clear analogy for their inward and outward curvatures. This article sets the stage for understanding key terminologies, such as the center of curvature and pole, laying the foundation for a comprehensive exploration of spherical mirrors and their distinct characteristics.
Spherical Mirrors and Their Types:
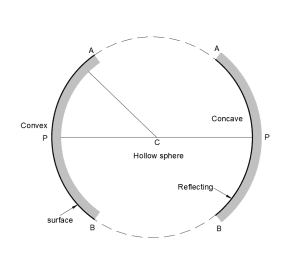
Imagine a glass with a hollow sphere featuring a reflective inner surface. This reflective hollow surface gives rise to spherical mirrors, which are categorized into two types: a) Concave Mirror and b) Convex Mirror. In the Concave Mirror, the reflecting surface curves inward, while in the Convex Mirror, the reflecting surface curves outward.
Centre of Curvature of Spherical Mirrors: The hollow sphere’s center, forming part of the spherical mirror, is termed the centre of curvature and is represented by the letter ‘C’.
Pole of Spherical Mirrors:
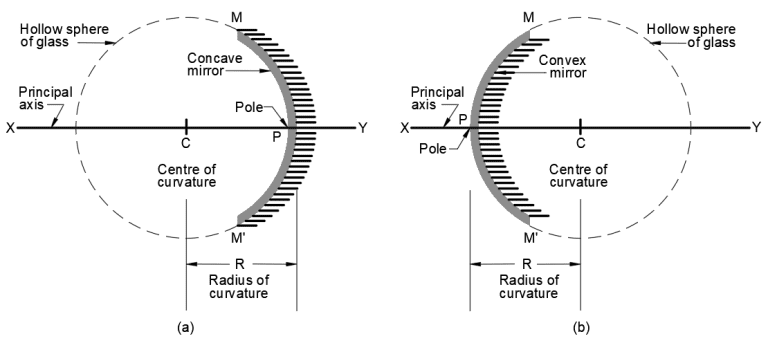
The pole of a spherical mirror is its central point, denoted by the letter ‘P’. It’s crucial to distinguish between the centre of curvature and the pole; the former is the center of the hollow sphere, whereas the latter is the center of the spherical mirror.
Radius of Curvature of Spherical Mirrors
The distance between the centre of curvature ‘C’ and the pole of the spherical mirror ‘P’ is known as the radius of curvature.
Principal Axis of a Spherical Mirror
The principal axis is a straight line that connects the pole of the spherical mirror and its centre. In the provided diagram, XY represents the principal axis.
Focal Length of a Mirror (f)
The focal length of a mirror is defined as half the distance of the radius of curvature, expressed as f = R/2, where f is the focal length and R is the radius of curvature.
Sign Conventions
The Cartesian Sign Conventions applied in deriving formulae for reflection and refraction by spherical mirrors and lenses adhere to the following principles:
- Distance measured in the direction of incident light is positive, and in the opposite direction, it is negative.
- Heights measured upward normal to the principal axis are positive, while heights measured downward are negative.
Mirror Equation
Consider the diagram with object AB at a distance ‘u’ from the pole. Rays AM, AP, and AN are reflected, converging to form an inverted image. The distance from the pole to this image, denoted as ‘v’, is the image distance. The mirror equation is expressed as:
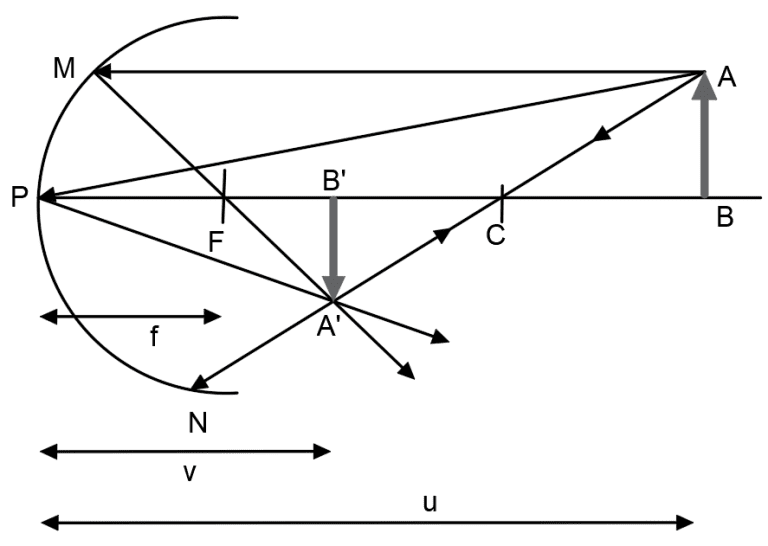
Let AB be an object and the distance of AB from the pole be ‘u’. ‘u’ is also known as object distance. An infinite number of rays travel from point A. But for time being let us consider only three rays that is, ray AM, AP and AN. The ray AN gets reflected back in the same direction that it travelled. As seen from the diagram the reflected rays of all the three rays intersect at a point where an inverted image of the object is formed. This is the real view of the original object. The distance at which the inverted image formed away from the pole is denoted by ‘v’. This distance is also known as Image Distance. Then the mirror equation is given by:
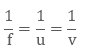
Conclusion
In summary, this exploration into spherical mirrors unfolds with a captivating invitation to visualize a glass sphere’s reflective inner surface, setting the stage for a comprehensive understanding of concave and convex mirrors. The article navigates through crucial terminologies such as center of curvature, pole, and radius of curvature, establishing a solid foundation. It further delves into the principal axis, focal length, sign conventions, and the mirror equation, demystifying the complexities of these mirrors. The inclusion of a practical example, illustrated through the mirror equation and diagram, enhances the practical application of theoretical concepts. This comprehensive guide equips readers with a profound comprehension of spherical mirrors, blending theoretical understanding with real-world relevance.
GREAT ARTICLE!
Share this article to gain insights from your connections!



